By far the most popular algorithm for Spaced Repetition is SM2. Sites like Anki, Duolingo, Memrise, and Wanikani all chose SM2 over later SM-iterations (eg. SM15) because it is extremely simple, yet effective. Despite that, it still has a number of glaring issues. In this article I explain those issues, and provide a simple way to resolve them.
Original SM2 Algorithm
The algorithm determines which items the user must review every day. To do that, it attaches the following data to every review-item:
- easiness:float – A number ≥ 1.3 representing how easy the item is, with 1.3 being the hardest. Defaults to 2.5
- consecutiveCorrectAnswers:int – How many times in a row the user has correctly answered this item
- nextDueDate:datetime – The next time this item needs to be reviewed
When the user wants to review, every item past its nextDueDate is queued. After the user reviews an item, they (or the software) give themselves a performanceRating on a scale from 0-5 (0=worst, 5=best). Set a cutoff for an answer being “correct” (defaults to 3). Then make the following changes to that item:
easiness += ![]()
consecutiveCorrectAnswers = 
nextDueDate = 
Problems with SM2
SM2 has a number of issues that limit its usefulness/effectiveness:
Problem: Non-generic variable ranges
The variable ranges are very specific to the original software, Supermemo. easiness is a number ≥ 1.3, while performanceRating is an integer from [0,5]
Solution
Normalize easiness and performanceRating to [0,1].
This requires setting a max value for easiness, which I set to 3.0. I also replaced easiness with difficulty, because it’s the more natural thing to measure.
Problem: Too many items per day
Because every day we do all the overdue items, it’s easy to encounter situations where one day you have only 5 items to review, and the next you have 50.
Solution
Only require doing the items that are the most overdue. Use “percentage” of due-date, rather than number of days, so that 3 days overdue is severe if the review cooldown was 1 day, but not severe if it was 6 months.
This allows review sessions to be small and quick. If the user has time, they can do multiple review sessions in a row. As a bonus, this allows “almost overdue” items to be reviewed, if the user has time.
Problem: Overdue items all treated equally
If the user completes a month-overdue item correctly, it’s likely they know it pretty well, so showing it again in 6 days is not helpful. They should get a bonus for correctly getting such overdue items correct.
Additionally, the above problem/solution allows almost-overdue items to be reviewed. These items should not be given full credit.
Solution
Weight the changes in due-date and difficulty by the item’s percentage overdue.
Problem: Items learned together are reviewed together
Items that are learned together and always correctly answered will always be reviewed together at the same time, in the same order. This hinders learning if they’re related.
Solution
Add a small amount of randomness to the algorithm.
Other adjustments
- The quadratic term in the difficulty equation is so small it can be replaced with a simpler linear equation without adversely affecting the algorithm
- Anki, Memrise, and others prefer an initial 3 days between due-dates, instead of 6. I’ve adjusted the equations to use that preference.
The Modified “SM2+” Algorithm
Here is the new algorithm, with all the above improvements in place.
For each review-item, store the following data:
- difficulty:float – How difficult the item is, from [0.0, 1.0]. Defaults to 0.3 (if the software has no way of determining a better default for an item)
- daysBetweenReviews:float – How many days should occur between review attempts for this item
- dateLastReviewed:datetime – The last time this item was reviewed
When the user wants to review items, choose the top 10~20 items, ordered descending by percentageOverdue (defined below), discarding items reviewed in the past 8 or so hours.
After an item is attempted, choose a performanceRating from [0.0, 1.0], with 1.0 being the best. Set a cutoff point for the answer being “correct” (default is 0.6). Then set
percentOverdue = 
difficulty += ![]()
difficultyWeight = ![]()
daysBetweenReviews *= 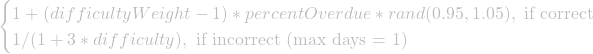
Daily Review Sessions
The above algorithm determines which items to review, but how should you handle the actual review?
That’s the topic for my next post – stay tuned!