The following is from an essay on Ramanujan I wrote a few years back. Enjoy.
…they recognized Ramanujan’s enormous talent for mathematics, and together they convinced Ramanujan to write to English mathematicians about his discoveries. […] The third letter he wrote, to M. J. M. Hill, received a reply, but was not very encouraging. In his reply, Hill stated,
“Mr. Ramanujan is evidently a man with a taste for Mathematics, and with some ability, but he has got on two wrong lines. He does not understand the precautions which have to be taken in dealing with divergent series, otherwise he could not have obtained the erroneous results you send me, viz:–
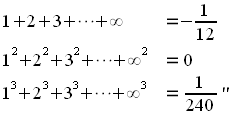
However, the problem was not with Ramanujan’s result itself, but rather with his lack of explanation of the result – or perhaps with Hill’s lack of knowledge on divergent series.
Before Ramanujan’s result can be explained, though, we have to first take a step back over 150 years in history. In 1749, the mathematics giant Leonhard Euler wrote a paper in which he derived the paradoxical result that 1 – 2 + 3 – 4 + … = 1/4.
Theorem (Euler) 1 – 2 + 3 – 4 + … = 1/4
Proof. Notice that the power series for 1/(x+1)2 is
![]()
If we assume this to be true for all x, we can plug in the value x=1 to obtain the desired result! ◊
In order for his result to make sense, Euler proposed (several times throughout his life) that an extended definition of the word “sum” be made. In his own words,
“Let us say, therefore, that the sum of any infinite series is the finite expression, by the expansion of which the series is generated. In this sense the sum of the infinite series 1 − x + x2 − x3 + … will be 1⁄1+x, because the series arises from the expansion of the fraction, whatever number is put in place of x. If this is agreed, the new definition of the word sum coincides with the ordinary meaning when a series converges; and since divergent series have no sum in the proper sense of the word, no inconvenience can arise from this new terminology. Finally, by means of this definition, we can preserve the utility of divergent series and defend their use from all objections.”
(It should be noted that Euler’s proof would not be valid by today’s standards, because 1 – 2x + 3x2 – 4x3 + … does not define a valid function when x=1. However, it would be valid to take the limit as x approaches 1 from the left; doing this yields the same result. Today there are many methods of finding the “sum” of a divergent series; the method just mentioned, laid out by Euler, is now known as the “Abel summation” of the series).
Now that we know what it means for a divergent series to “sum” to a certain finite value, we can ask the question of whether or not Ramanujan’s results were in any way correct.
Theorem 1+2+3+…+∞ = -1/12
Proof. This proof is due to Ramanujan – though he didn’t send it to Hill originally, he did write it down in his first notebook.
Say we set c = 1 + 2 + 3 + … Then
![]()
Subtracting the bottom row from the top,
![]()
ala Euler. Thus, c = -1/12. This result is correct to the extent that Euler’s result is correct as well. ◊


One Comment
Thanks to your post I now understand the meaning of these divergent sums.